
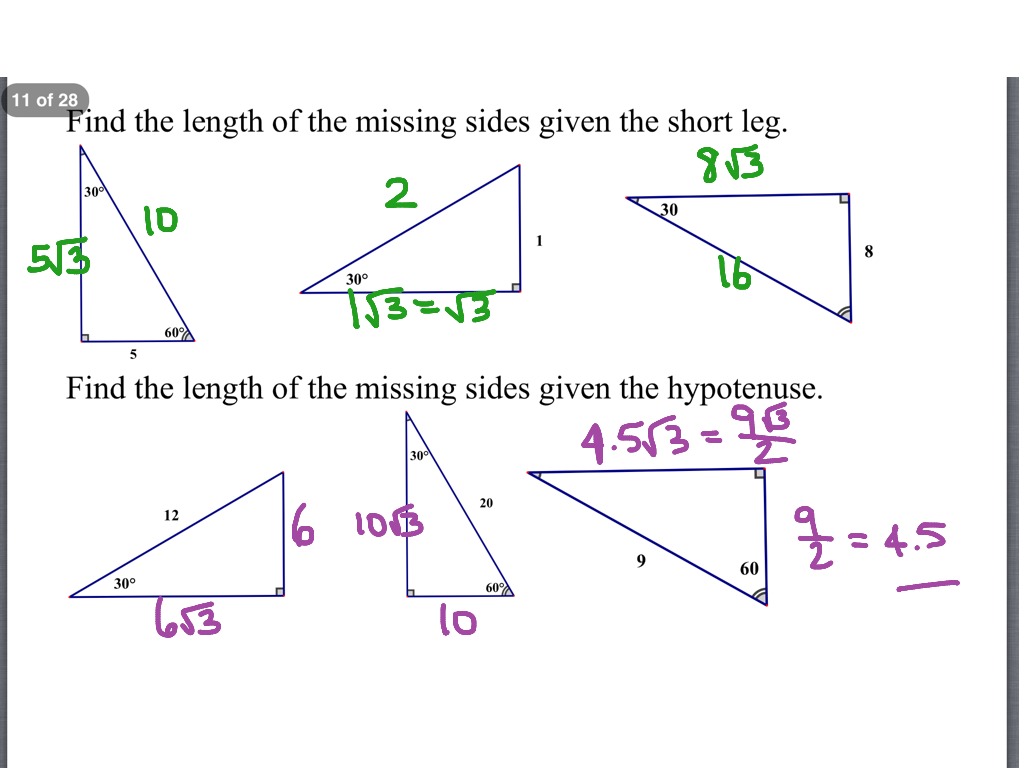
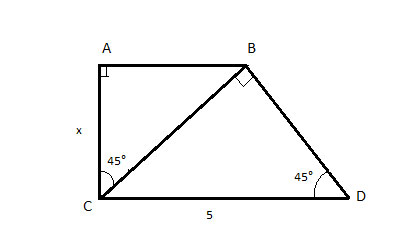
Let us understand the concept better by doing some practice problems. Instead of using the Pythagorean Theorem, we can simply use the special right triangle ratios to find the missing length. Solving special right triangles is about finding the missing lengths of the sides. Find their formulas with solved examples in our separate articles. Special Right Triangle Overview with Examples Powered by Create your own unique website with customizable templates. The ratio x : x : x for isosceles right triangles can now be applied. Figure 3 A diagonal of a square helps create two congruent isosceles right triangles. Method 1: The diagonal of a square divides it into two congruent isosceles right triangles.Look at Figure 3.
Sides that are in Geometric Progression: Also known as the Kepler triangle, if the sides are in geometric progression a, ar, ar 2, its common ratio r is given by r = √φ where φ is the golden ratio.Īlthough there is no common formula for special right triangles, each of them has specific formulas for finding the missing sides, area, and perimeter based on the ratio of their side lengths. 30-60-90 Triangle - Explanation and Practice Problems 30-60-90 Triangle Example Notes 45-45-90 Triangles. Example 2: If the diagonal of a square is 6, find the length of each of its sides.When all students have finished filling in the lengths of the missing sides, I ask for volunteers to present the answers to each problem. Examples – 20-21-29, 119- 120-169, 696-697-985, and 4,059-4,060-5,741. These problems are designed to help them recall the three types of special triangles that they have learned: Pythagorean triplets. Almost-isosceles Pythagorean Triples: Sides with integer lengths but almost isosceles.Common Pythagorean triples: Sides with integer lengths.Pythagorean triples can be of three types: Such triangles can be easily remembered and any multiple of the sides produces the same relationship.

Some right triangles have sides that are of integer lengths and are collectively called the Pythagorean triples. The ratio of its side lengths (base: height: hypotenuse) is1: √3: 2.Īpart from the above two types, there are some other special right triangles. Give two examples: one where the resulting equation has the. A 30-60-90 triangle is a special right triangle with some very special. Help the class to come up with a list of steps for solving right triangle trigonometry problems. 30-60-90 TriangleĪ 30-60-90triangle is a special right triangle whose three angles measure 30°, 60° and 90°. problem example 30 60 90 triangle right triangle missing leg missing side. The ratio of its side lengths (base: height: hypotenuse) is 1: 1: √2. A 45-45-90 triangle is one type of special. So another name for an isosceles right triangle is a 45-45-90 triangle. Since the base angles of an isosceles triangle are congruent, the measure of each acute angle is 45. The two most common special right triangles are: 45-45-90 TriangleĪ 45-45-90 triangle is a special right triangle whose three angles measure 45°, 45° and 90°. 5-8 Applying Special Right Triangles A diagonal of a square divides it into two congruent isosceles right triangles.
Leave your answers as radicals in simplest form. This is a right triangle with two equal sides.Special Right Triangles Types of Special Right Triangle Special Right Triangles Date Period Find the missing side lengths.

+ The Ultimate FTCE General Knowledge Math Course.+ FTCE General Knowledge Math Worksheets.


 0 kommentar(er)
0 kommentar(er)
